都留本部校･東桂校『土曜日は合否判定模試！』2024.1.18

都留･東桂校小澤です。

本日は都留校での通常授業となります。 (*’▽’)/
また、今週末の1/20(土)は、中学生全学年を対象として『合否判定模試』を行います。
それに伴い、中学3年生の受験対策授業と中学生全学年の理社オンライン授業はお休みとなります。
配布済みの予定表をご確認いただき、お間違いの無いようにお願いします。 m(_ _)m
ご不明な点は校舎までお問い合わせください。

★ おまけ ★
昨日の「Advanced鷹匠校の山西先生からのお題」の解答です。

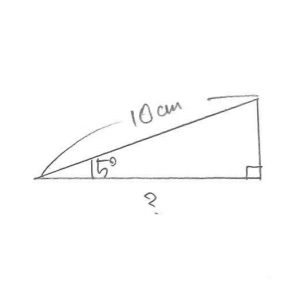
この三角形の面積を求める問題です！ (@_@)

① まず、小学6年生でも解ける？考え方です。

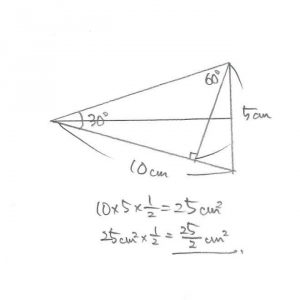
出題された三角形の下側に、それと合同な三角形を裏返しにして書き込みます。
できた図形の右上の頂点から対辺に「垂線(90度になる線)」を下ろします。
その時にできる角度のうち、ポイントとなるモノを図に書き込みましたが･･･
内角が90度･60度･30度の直角三角形って、正三角形を半分にした形なので、さっき下ろした垂線の長さは5㎝であることがわかります。
だから、図形全体の面積は25㎠。出題された図形はその半分なので25/2㎠となります。 (@_@)

② 中学3年生で「理数科合格クラス」に参加した人なら、こんな考え方もできるのではないでしょうか？

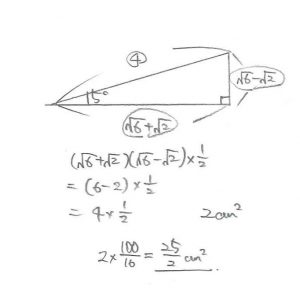
三角形の「辺の比」です。通常クラスでも授業内で伝えてはありますが、練習問題をこなしていないのでキツイかもしれません。。。
ひとつの鋭角が15度である直角三角形は、図のような位置関係で「4:(√6＋√2):(√6−√2)」となっています。
斜辺を4㎝としたときの面積は、(√6＋√2)×(√6−√2)÷2＝2㎠となります。
出題されたコレと相似な三角形は斜辺の長さが10㎝なので、面積比は「16:100」です。
なので、2㎠×100/16=25/2㎠となります。 (*’▽’)/

中学3年生のみなさん、高校入試に出題されてもおかしくない問題です。三角形の辺の比で「1:2:√3」と「1:1:√2」はすでに使いこなせていると思いますが、うまい具合に補助線を入れたりしないと解けないかもしれません。
余裕のある人は「4:(√6＋√2):(√6−√2)」も使えるようにしておきましょうね！ (*’ω’*)

▲ 河口湖校の健Tは正解しました！